Hoy es 29 de febrero de 2016, estamos en año bisiesto y realizamos el desembolso inicial de una inversión por importe de 770.000 €. Se obtienen 5 recuperaciones de 310.228 € cada una que vencen en los próximos 29 de febrero de los próximos años bisiestos. Calcular la TIR de la operación.
Calcular el valor actual que se obtiene valorando al 9,0% efectivo anual el conjunto de las dos siguientes rentas. Renta A: Duración 15 años, términos semestrales pospagables de 8.800 € Renta B: 48 términos trimestrales de 9.300 €, abonándose el primero junto al 7º término de la renta A.
Un inversor deposita en un banco 753.000 € a 9 años con pago mensual de intereses al 12,0% nominal anual. Los intereses se ingresan en otra cuenta que proporciona un 5,30% efectivo anual. Calcular la rentabilidad obtenida por el inversor a lo largo de estos 9 años, por su 753.000 €, expresada en tanto efectivo anual.
El Sr. A adquiere una Letra del Tesoro en el mercado primario por 945,0 € a un vencimiento de 12 meses. Transcurridos 4 meses compra otra Letra de la misma emisión por un precio de 956,0 €. Transcurridos 4 meses más vende ambas Letras a un segundo inversor, el Sr. B, que mantiene las Letras hasta su vencimiento. El Sr. B obtiene una rentabilidad del 6,0% efectivo anual. Calcular la rentabilidad obtenida por el Sr. A, expresada en tanto efectivo anual.
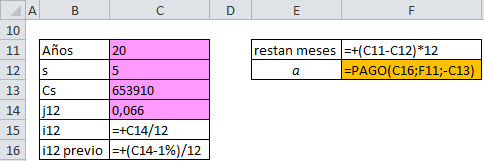
Se contrató un préstamo de principal Co a un plazo de 20 años, amortizable mediante términos amortizativos mensuales y a tipo de interés variable con revisión anual. Al final del año 5 el capital vivo es de 653.910 €, y el nuevo tipo de interés anunciado en ese momento es del 6,60% nominal anual, que ha resultado ser mayor en un punto al anuanciado justo hace un año. Calcular la mensualidad que vence justo al final del año 5.
Dª. Rosalia contrata una cuenta bancaria en la que ingresa cada trimestre 5.600 € durante 5 años. La cuenta proporciona una rentabilidad del 8,50% efectivo anual. También realiza en la cuenta 10 disposiciones semestrales constantes de importe C, realizándose la primera de ellas justo 2 meses después de haber realizado la aportación 5ª. Calcular C sabiendo que al retirar la última disposición la cuenta se pudo cancelar con saldo cero.
Calcular el tanto medio de una operación de capitalización expresado en tanto efectivo anual. La operación financiera parte de un capital inicial C que durante el primer año se capitaliza al 4,70% efectivo semestral, durante el segundo año se capitaliza al 9,90% nominal anual con pago de intereses mensual. Durante los años 3º y 4º se capitaliza al 0,85% efectivo mensual, y durante el quinto año se capitaliza al 2,70% efectivo trimestral.
En un mercado de renta fija conocemos cuatro puntos de la ETTI. A un año es r01=7,410%, a dos años es r02=8,458%, a tres años es r03=9,845% y a cuatro años es r04=11,750%. Calcular la duración de Macaulay de una cartera que está compuesta por 8 bonos cupón cero a un año, 13 bonos cupón cero a dos años, 15 bonos cupón cero a tres años, y 18 bonos cupón cero a 4 años.
Podemos encontrar los siguientes bonos en el mercado de renta fija. * Bono A: bono a cuatro años, cupón explícito anual del 6,40%, nominal 5.000 € y precio 3.766,42 €. * Bono B: bono a cuatro años, cupón explícito anual del 14,30%, nominal 9.000 € y precio 8.863,84 €. * Bono C: bono a cuatro años, cupón explícito anual del 17,0%, nominal 1.000 €. Calcular el precio del bono C, conocidos tres puntos de la ETTI a 1, 2 y 3 años, que respectivamente son r01=11,010% , r02=12,341% y r03=14,132%.
Agustín y Begoña adquieren una casa por 689.000 € que financian al 100% mediante un préstamo hipotecario a 16 años con pagos mensuales. El tipo de interés es constante del 6,0% nominal anual. Agustín paga las mensualidades de los 8 primeros años por importe de a euros, y Begoña paga las mensualidades de los últimos 8 años por importe de b euros. Calcular en que porcentaje ha de ser mayor b que a, para que ambos paguen la casa a partes iguales.
Se contrata un préstamo a 12 años al 11,0% anual, cuyo principal es 534.000 €, amortizado mediante cuotas de amortización anuales constantes. Calcular el término amortizativo del 9º año.
Se contrata un préstamo americano de términos mensuales y tipo de interés constante del 11,20% efectivo anual, sobre un principal de 523.000 € a un plazo de 8 años. Simultáneamente y asociado al préstamo se contrata un fondo de constitución de capital con el fin de llegar a amortizar el principal del préstamo al final del 8º año. El fondo retribuye las aportaciones al mismo tipo de interés al que se contrata el préstamo, siendo las aportaciones constantes, mensuales y pospagables. Calcular la mensualidad conjunta que se ha de abonar por ambas operaciones.
Se contrata un préstamo americano de términos anuales y tipo de interés constante del 8,50% anual, sobre un principal de 951.000 € a un plazo de 8 años. Simultáneamente y asociado al préstamo se contrata un fondo de constitución de capital con el fin de llegar a amortizar el principal del préstamo al final del 8º año. Se realizan aportaciones pospagables mensuales constantes al fondo que retribuye las aportaciones realizadas al 3,80% efectivo anual. Calcular la reserva matemática por la derecha de la operación conjunta al final del 5º año.
