Dos bonos se amortizan en la misma fecha, dentro de 3 años. Ambos bonos se pueden adquirir hoy a la par: el bono A por 10.000 € y el bono B por 15.000 €. Ambos proporcionan un cupón anual, el bono A del 5,0% y el bono B del 6,0%. El bono A tiene una prima de amortización de 900 €. Se pide calcular la TIR de un bono cupón cero a tres años que se adquiera en la misma fecha que los otros dos bonos.
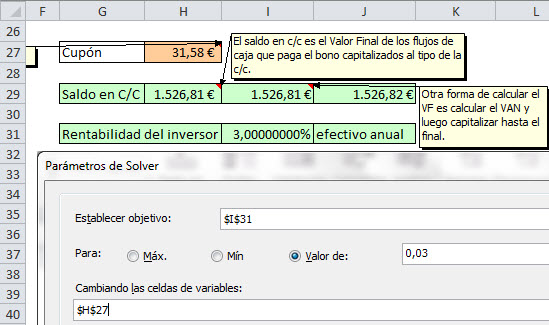
Un bono se emite en el mercado primario por 980 €. El bono es de 1.000 € nominales y proporciona un cupón de C € anuales durante 15 años, amortizándose por el nominal. Un inversor que adquiere el bono ingresa todos los cupones en una cuenta corriente bancaria que proporciona una rentabilidad del 1,50% efectivo anual. Si el inversor obtiene una rentabilidad del 3,0% efectivo anual durante los 15 años por sus 980 €, determinar el importe del cupón.
En el mercado están disponibles los siguientes bonos: • Bono A: Letra del tesoro de duración un año y precio de adquisición 933,0 €. • Bono B: Bono cupón explícito del 7,0% y duración 2 años que se adquiere con un descuento del 2,0% sobre el nominal. Determinar el tipo de interés forward implícito para el periodo que se inicia en t=1 y finaliza en t=2 años.
En el mercado cotizan los siguientes bonos:
* El bono A es un Bono Cupón Cero con vencimiento a un año y TIR del 5,0%.
* El bono B es un Bono Cupón Cero a dos años y TIR del 6,0%.
* El bono C es un Bono Cupón Explícito del 3,0% anual a 3 años, que se adquiere por 905,0 € y se amortiza por el nominal que es de 1.000 €.
* El bono D es un Bono Cupón Cero a 4 años y TIR del 7,0%.
Determinar la TIR de un Bono Cupón Explícito del 8,0% anual a 4 años.
Deseamos disponer de una maquinaria mediante una operación de leasing. El principal es de 900.000 €, se financia a 3 años mediante pagos trimestrales prepagables y el valor residual supone una trimestralidad más. El tipo de interés nominal anual pactado es del 5,40%. Nos aplican un IVA del 21%. Calcular el importe que hemos de pagar por una cuota trimestral.
De un préstamo francés sabemos que se contrató a un plazo de n trimestres, a un tipo fijo del 8,0% TIN. El capital vivo al final del trimestre 37 es de 659.000 €, y la trimestralidad es de 15.063,21 €. Calcular el capital vivo al final del trimestre 120.
Se concede un préstamo francés a 25 años, por importe de 700.000 €, a un TIN del 6,30%, con pagos mensuales. Transcurridos 50 meses se renegocian las condicioes del contrato. En lo sucesivo se aplicará un tanto efectivo anual del 5,0%, y se acortará la duración total del préstamo en 20 meses. Calcular la nueva mensualidad que surge después de la renegociación.
Se contrata un préstamo de principal 637.000 €, a tipo variable (Euribor+0,40%) con revisión anual y una duración de 19 años. Los dos primeros años el Euribor ha resultado ser del 5% y 6% respectivamente. El prestatario realizó una amortización anticipada de 87.000 € al final del mes 15, sin coste y sin reducir la duración total del préstamo. Calcular la mensualidad del mes 16.
Un préstamo se contrató con las siguientes características: Principal: 640.000 €. Duración: 26 años, con pagos mensuales. Tipo variable: Euribor + 0,70% con revisión anual. Han transcurrido tres años, y los Euribor han sido: 2,70%, 2,90% y 3,40% para los años 1, 2 y 3 respectivamente. Para el próximo año se anuncia un Euribor del 4,40%. Considerar todos los tantos como TIN. Los dos primeros años fueron de carencia, donde se pagaban unicamente los intereses. Calcular la próxima mensualidad.
Un préstamo a tipo variable (Euribor+0,21%) con revisión anual, se contrata a 7 años, por 856.000 €. El Euribor durante los 2 primeros años ha sido del 7,60%, durante los 2 siguientes del 2,20%, y durante los 3 restantes del 5,10%. Calcular el importe de la mensualidad del mes 38.
Un préstamo francés de 1.500.000 €, a 6 años, con términos trimestrales se pacta al 8% TIN. El banco nos permite efectuar amortizaciónes anticipadas sin cobrarnos ninguna comisión. Las aportaciones adicionales que realicemos reducirán la trimestralidad y no alterarán la duración total del préstamo. Calcular la última trimestralidad si decidimos amortizar anticipadamente 14.000 € al final del segundo trimestre de cada año.
Un préstamo de principal 300.000 €, que se contrató al 9% nominal anual, debe reembolsarse mediante n entregas semestrales constantes (a). El capital vivo del semestre n-5 asciende a 101.245,35 €. Calcular a.
Un inmueble de precio P se financia en un 75% mediante el pago de dos préstamos A y B. El préstamo A supone pagos de 900 € al trimestre durante 20 años, abonándose la primera cuantía al trimestre de firmado el contrato. El préstamo B supone 30 pagos semestrales de 32.000 €, abonándose la primera cuantía junto con la décima trimestralidad de 900 €. El tipo de interés para ambos préstamos es del 12,0% efectivo anual. Calcular el precio del inmueble.
