Préstamo francés convertido en italiano

Un préstamo de principal 100.000 € se contrató hace un año al 4% nominal anual, con pagos trimestrales constantes de 2.820,44 €. Ya se han pagado en este momento los cuatro primeros términos amortizativos y se procede a renegociar las condiciones. Se acuerda que en el futuro las cuotas de amortización trimestrales serán constantes de importe A. El capital vivo dentro de un trimestre será de 90.293,08 €. Calcular la duración total del préstamo.

---

Ejercicio resuelto

Ley de variación de las cuotas de amortización en un préstamo francés

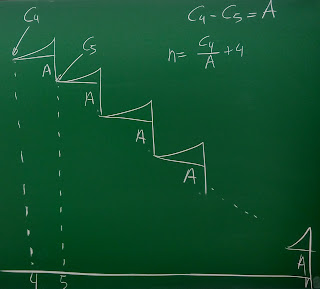
Partimos del gráfico del esquema dinámico de un periodo genérico s, el periodo s-ésimo, que comienza en el instante t=s-1 y finaliza en el instante t=s.

Siguiendo el gráfico podemos establecer la anterior ecuación.

Planteamos la ecuación anterior para un préstamo francés donde el término amortizativo es contante de importe a.

Sobre la ecuación anterior ponemos la que corresponde a un periodo anterior y restamos ambas.

Obtenemos la denominada ley de variación de las cuotas de amortización de un préstamo francés, que podemos expresar con las siguientes palabras.

En un préstamo francés las cuotas de amortización crecen en progresión geométrica de razón (1+i).

Nos interesa obtener una fórmula que relacione una cuota de amortización genérica A_s con la primera de ellas A₁.

Para hacer operativa la ley anterior nos interesaría conocer la primera cuota de amortización A₁.

Para conocer A₁ disponemos de dos métodos.

Recordemos cómo es el valor final de una renta unitaria pospagable.

Veamos el segundo método para calcular A₁.

Cuadro de amortización

Puede descargar el archivo cuadroAmortizacion.xlsx

Al estudiar todas las magnitudes de un préstamo a lo largo del tiempo, se realiza un cuadro denominado cuadro de amortización.

Préstamo Italiano

Se caracteriza porque la cuota de amortización es contante A=cte.

Préstamo Francés

Se caracteriza porque el término amortizativo es contante a=cte.

Coinciden A_n y C_n-1

Audio