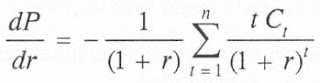Francés con pocos datos

Puede descargar el archivo de Excel frances_escaso.xlsx

Este es un ejemplo que permite comprobar la enorme utilidad de Solver en el campo financiero. Con escasos datos conseguimos completar el cuadro de amortización de un préstamo francés.

Esta es una solución analítica: frances_con_pocos_datos.pdf

Sensibilidad de un Bono

Cuando hablamos de Sensibilidad de un Bono nos referimos a la Sensibilidad del Bono respecto a los tipos de interés. Queremos saber cómo se comportará el precio de un bono ante las variaciones de su rentabilidad medida por su TIR.

Sabemos que precio (P) y rentabilidad (r) se mueven en sentido contrario, pero nos gustaría saber en que magnitud. Nos gustaría poder comparar dos bonos y saber cuál de ellos es más sensible.

 La curva siguiente nos muestra el comportamiento de estas dos magnitudes: Precio y Rentabilidad.

Esta curva no es una línea recta, por lo que no existe proporcionalidad o linealidad entre ambas magnitudes. Pero podemos tomar una aproximación lineal a la curva. Para ello tenemos que utilizar algo la matemáticas. Tenemos que derivar en una variable.

El precio de un bono es:

donde

• Ct son los Flujos de Caja que paga el Bono desde t=1 hasta t=n.
• r es la rentabilidad del Bono medida por su TIR

Ahora derivamos el Precio (P) respecto a la TIR (r).

puesto que sabemos que la Duración es:

podemos obtener la siguiente expresión:

El término de la izquierda dP/P es la variación porcentual del Precio.
D es la Duración de Macaulay
D/(1+r) es la denominada Duración Modificada
dr es la variación de la rentabilidad
Y el signo menos es importante, ya que nos indica que precio y rentabilidad se mueven en sentido contrario.

A efectos de aplicación práctica, los diferenciales anteriores se toman como incrementos, y así obtenemos una expresión, que ya no es una igualdad sino una expresión en términos aproximados.

La expresión anterior se puede leer en palabras de la siguiente forma:

La variación porcentual del precio en un bono es aproximadamente igual a la duración modificada multiplicado por la inversa de la variación de su rentabilidad.

La aproximación es tanto mejor cuanto menor sea la variación de la TIR que tomemos.

Gráficamente lo que estamos haciendo es la típica aproximación lineal a una curva en un punto, que es lo que vimos en su día cuando nos explicaron el concepto de derivada.

En la práctica financiera se toman centésimas partes de punto 1%/100, que se denomina punto básico.

1 pb = 1% / 100

Un punto porcentual son 100 puntos básicos (100 pb).

Pongamos un ejemplo. Supongamos que un bono, cuya duración modificada es 3, experimenta una reducción en su rentabilidad de un 1%, esto es, 100 pb. En este caso la variación porcentual del precio es:

∆P/P ≈ - 3 * (-1%) = 3%

Esto quiere decir que la variación porcentual del precio (∆P/P) es del 3%. Por tanto, en términos aproximados el precio del bono se incrementa un 3% por cada 1% que caiga su rentabilidad.

Vemos perfectamente, gracias al signo menos, que precio y rentabilidad se mueven en sentido contrario.

Además, estamos comprobando que la duración modificada (D/(1+r)) hace el papel de multiplicador y que simplemente conociendo su valor podemos comparar dos bonos. De esta forma, si tenemos un bono, como el anterior, que llamaremos Bono A, cuya duración modificada de 3, y otro, Bono B, que la tiene de 10, es claro que el de mayor duración modificada será el más sensible. El Bono B ante una reducción del 1% en su TIR, experimentará un incremento porcentual del Precio del 10%, aproximadamente.

Estos sencillos cálculos mentales, permiten a los operadores de Renta Fija, conocer la sensibilidad de un bono simplemente mirando las pantallas de Reuters o de Bloomberg que les proporcionan este dato.

Duración de Macaulay

Puede descargar el archivo de Excel v_bonos06.xlsx

La Duración de Macaulay es un concepto que mide la duración media de un Bono. Es una media que se obtiene ponderando por el peso de los diferentes flujos de caja descontados.

La fórmula es:

r es la TIR del bono

Ct son los flujos de caja en cada instante t, desde t=1 hasta t=n.

El denominador es el Precio del Bono.

El numerador es muy parecido al denominador. Simplemente se ha de multiplicar por t, que es el tiempo. De esta forma los flujos de caja descontados actúan como ponderador.

La Duración de Macaulay, o simplemente Duración, es la típica fórmula de la media ponderada, y la unidad temporal en la que viene dada son años, si los flujos son anuales. Si los flujos fueran mensuales, tendríamos que trabajar con la TIR mensual y en ese caso la duración resultante vendría expresada en meses.

La Duración Modificada es igual a la duración de Macaulay dividida entre (1+r), siendo r la TIR del bono. Es útil para medir la Sensibilidad del Bono ante las variaciones de los tipos de interés. Será más sensible aquel bono de mayor duración.

Si usted prevé que las rentabilidades del mercado de renta fija caerán, ¿en que bono invertirá?, ¿en uno de corta duración o en otro de larga duración?. Puesto que precio y rentabilidad se mueven en sentido contrario, si la rentabilidad cae, sube el precio, por tanto nos interesará invertir en el bono de mayor duración, para aprovechar una mayor subida del precio. Pero si nos equivocamos en nuestras previsiones, el precio caerá, y lo hará de forma más acusada el precio del bono de mayor duración. Por eso, decimos que el bono de mayor duración es más sensible ante las variaciones de los tipos de interés.

Replica de un Bono cupón explícito

Vamos a calcular el precio de un Bono C, conocidos los Bonos A y B que nos dan dos puntos de la ETTI por ser Bonos Cupón Cero.

Un Bono Cupón Cero es un bono que no paga cupón intermedio. Por ejemplo, una Letra del Tesoro. Únicamente existe un Co en t=0, y un Cn en t=n, y ningún otro Flujo de Caja.

Un Bono Cupón Explícito es un bono que paga cupón periódico, y por tanto no es un Bono Cupón Cero.

La ETTI es la Estructura Temporal de los Tipos de Interés, y se forma exclusivamente con las rentabilidades (las TIR) de los Bonos Cupón Cero a los diferentes plazos.

En nuestro caso:

1. El Bono A es un bono cupón cero a un año, cuya TIR es del 10%. Por lo que ya conocemos un punto de la ETTI, justo a un año.
2. El Bono B es un bono cupón cero a dos años, cuya TIR es del 11,0555%. Por lo que ya conocemos otro punto de la ETTI, justo a dos años.

Primero vamos a valorar usando la ETTI. Calcularemos el precio del Bono C y su TIR.

Aquí se aprecia que la TIR (r) es una media de las rentabilidades a los diferentes plazos. La TIR del bono C necesariamente ha de estar entre el 10% y el 11,0555%. Ha salido justo de un 11%. Esta más cerca de r02 que de r01, ya que la TIR es una media de rentabilidades, pero ponderada por el peso que tengan los flujos de da caja descontados del bono. Y en el caso del bono C pesa mucho más el último flujo de caja, por eso la TIR queda mucho más cerca de r02.

Ahora vamos a valorar utilizando una combinación de los Bonos A y B para llegar a obtener el Bono C. Estamos efectuando la réplica el Bono C y para ello utilizamos los bonos A y B que cotizan el el mercado.

Préstamo a tipo variable

Puede descargar el archivo de Excel v_frances3.xls

La mayoría de los préstamos actualmente se contratan a tipo variable, en especial los de largo plazo, como los préstamos hipotecarios. Si usted solicita un préstamo hipotecario es muy probable que esté considerando contratar tipo variable, ya que el tipo aplicado inicialmente es menor. En muchos bancos, ni siquiera le ofrecerán un préstamo hipotecario a tipo fijo.

Para entender cómo funciona un préstamo a tipo variable vamos a resolver un caso sencillo trabajando en años, y posteriormente lo iremos complicando haciéndolo más realista.

Podemos calcular C4 usando la función VA de Excel.

Podemos calcular a' usando la función PAGO de Excel.

Cómo mejorar la precisión de Solver

Solver utiliza un algoritmo de cálculo que le da mucha mayor precisión que a 'Buscar Objetivo'. Pero puede que en algunos casos necesitemos mejorar la precisión de Solver, en especial cuando en los cálculos esta implicada la TIR.
Para mejorar la precisión de Solver efectuaremos estos pasos:

1. En la ventana de Solver, pulsamos sobre el botón: "Opciones..."
2. Veremos una imagen como esta
   
   
   
   
   
   
3. En "Precisión:" metemos un par de ceros más. Si ponia: 0,00000001, ahora pondrá: 0,0000000001.
4. Aceptamos y resolvermos con Solver

Si todo ha ido bien, veremos que la precisión de nuestros cálculos han mejorado.

Leyes Financieras Clásicas

Ejemplo de operación de CAPITALIZACIÓN

Tengo un capital inicial Co que deseo invertir durante un tiempo de n años. Voy al banco y solicito un depósito a tipo fijo (i). Transcurrido el plazo recibo el montante Cn. Si he pactado capitalización compuesta obtengo:
Cn=Co(1+i)^n

Ejemplo de operación de DESCUENTO

Una empresa no cobra a sus clientes al contado. Esta es la práctica más habitual en las empresas. Supongamos que pagará dentro de n años (normalmente días: 30, 60, 90, 120, 180 o 270 días). La empresa necesita liquidez y no puede (o no desea) esperar hasta su vencimiento para obtener el dinero. Para conseguir adelantar el cobro, se acerca a su banco y solicita que descuenten esa letra de cambio, o factura (cualquier documento válido en el que esté documentado el derecho de cobro). El banco está dispuesto a adelantar el dinero del cobro a cambio de un cierto beneficio para él. Este margen se materializa en la aplicación de un tanto de descuento d. Normalmente se opera aplicando descuento simple comercial. El efectivo que se obtiene (E=Co) es inferior al nominal de la letra de cambio o factura (N=Cn). La fórmula que aplica el banco para obtener el efectivo es:
Co=Cn(1-dn)

Podrían haber aplicado un tanto i, pero la costumbre de la banca es trabajar con una tanto d, en capitalización simple, que es lo que se denomina descuento simple comercial.
Normalmente se trabaja en días, por ejemplo 90 días, y se aplica año comercial (base 360). Si el nominal a descontar fuera de 10.000 euros, y el tanto de descuento fuera del 8%, el efectivo pecibido sería:
Co=Cn(1-d*días/360)
Co=10000(1-0,08*90/360)=9.800 euros.
El descuento D (en euros) aplicado por el banco ha sido:
D=Cn-Co=10.000-9.800=200 euros.
Esos 200 euros es lo que esta pagando la empresa por anticipar el pago, Esto es, para evitar esperar 90 días al cobro de los 10.000 euros, la empresa está dispuesta a pagar 200 al banco.
Esos 200 euros son el coste por anticipar el pago, pero no cubre el riesgo de impago. Esto es, si el cliente llegado el plazo no paga, el banco no es el que asume el impago, sino la empresa. Si se desea cubrir el riesgo de impago el banco no tendrá inconveniente en cubrir ese riesgo, pero eso supondrá un  nuevo contrato de seguro de pago, con un nuevo coste. Los 200 euros únicamente cubren el anticipo del pago.

Normalmente las empresas utilizan este método de financiación, que por otro lado es bastante caro. Una alternativa podría ser disponer de una 'línea de crédito' para cubrir los picos de tesorería. Pero ese es otro tema.
A efectos de estudio se ve la capitalización simple a tanto i, que es lo que se denomina descuento simple racional o matemático. Pero esto es únicamente a efectos de comparación y de completar el estudio teórico, ya que el que se usa en la práctica financiera es el DESCUENTO SIMPLE COMERCIAL, y normalmente en base 360 (año comercial), que si te das cuenta es el que beneficia a la banca.

Analicemos las leyes financieras clásicas

La ley de capitalización compuesta es: Cn=Co(1+i)^n
Despejando Co obtienes la ley de descuento a tanto de interés i:
Co=Cn/(1+i)^n
que se suele expresar como:
Co=Cn(1+i)^-n

La ley de descuento compuesto compuesto a tanto de descuento d es:
Co=Cn(1-d)^n
Esta ley no se usa nunca, se pone habitualmente para completar el cuadro, pero en la práctica financiera nadie la usa.

La ley de capitalización simple es:
Cn=Co(1+in)

Si despejas Co se obtiene la ley de descuento simple a tanto de interés i, también denominada ley de descuento simple racional o matemático, es que:
Co=Cn/(1+in)
El descuento simple racional habitualmente no se usa en la práctica financiera. Se pone en la tabla para completar, y existe para dar coherencia la descuento simple comercial que tiene incoherencias internas importantes (como por ejemplo, que aplicado con tipos altos y a largo plazo puede llegar a dar lugar a Efectivos incluso negativos).

El que se utiliza en la práctica financiera es el descuento simple a tanto de descuento d, o también conocido como descuento simple comercial. Este pese a sus incoherencias es el que se usa ya que se utiliza a corto plazo. Se usa porque es el que beneficia a la banca. Su expresión es:
Co=Cn(1-dn)

• Si se trabaja en meses la fórmula es: Co=Cn(1-d*meses/12)
• Si se trabaja en días la fórmula es: Co=Cn(1-d*días/base)

• Si la base = 365 decimos que trabajamos con año civil.
• Si la base = 360 decimos que trabajamos con año comercial.

Audio

Forward

En un mercado cotizan los bonos siguientes:
Bono A: Es un bono cupón cero a un año, TIR del 10%
Bono B: Es un bono a dos años que paga un cupón del 9% anual, TIR del 9,5%
Bono C: Es un bono a tres años que paga un cupón del 8% anual, TIR del 8,5%
Bono D: Es un bono a cuatro años que paga un cupón del 7% anual, TIR del 8%.
Calcular el tipo forward implícito r34 (con inicio en t=3 y final en t=4 años).

---

Método 1

Calculamos los precios de los bonos B, C y D con VAN o con VA, sabiendo sus flujos y sus TIR.

Para calcular r34 utilizamos la fórmula:

Por tanto, necesitamos conocer  r03 y r04 que son los puntos de la ETTI a 3 y 4 años. Son las rentabilidades de los bonos cupón cero a 3 y 4 años. Pero el enunciado nos da los bonos C y D, a 3 y 4 años, respectivamente pero como bonos de cupón explícito.

Necesitamos ir construyendo los cuatro puntos de la ETTI r01, r02 r03 y r04 de forma progresiva, ya que para conocer uno de ellos necesitamos los anteriores. El primero (r01) es sencillo ya que es la TIR del bono A, por tratarse de un bono cupón cero a un año.

• Para calcular r02, planteamos la ecuación que calcularía el precio del bono B (bono a dos años), usando la ETTI. Pero el precio el bono ya le conocemos, por lo que la única incógnita es r02.

• Para calcular r03, planteamos la ecuación que calcularía el precio del bono C (bono a tres años), usando la ETTI. Pero el precio el bono ya le conocemos, por lo que la única incógnita es r03.

• Para calcular r04, planteamos la ecuación que calcularía el precio del bono D (bono a cuatro años), usando la ETTI. Pero el precio el bono ya le conocemos, por lo que la única incógnita es r04.

Método 2

Con Solver, este problema, es mucho más fácil de resolver.

La celda G31 es:

=SUMAPRODUCTO($C$29:$F$29;C31:F31)

y luego se copia hacia abajo, para todos los flujos de caja del bono E.

Luego pedimos a Solver que haga cero todas las celdas amarillas, para así conseguir que el bono E sea un bono Forward r34. Como Solver solo admite una función objetivo, elegimos una de las celdas amarillas como objetivo, y el resto irá en las restricciones.

Si todo va bien, Solver encontrará en las celdas grises la combinación adecuada de los bonos A, B, C y D necesarios para conseguir nuestro propósito.

¿Qué son las celdas grises?

Las celdas grises nos dan la proporción en la que se han de combinar dos o más bonos para obtener un tercero. El valor que alzanzan esas celdas grises no es importantes, lo interesante es que hemos llegado a crear un bono sintético combinando otros bonos en determinada proporción. Si la celda gris que acompaña a un bono A es 2 positivo indica que hemos de comprar dos bonos A, y si la celda gris que acompaña al bono B es -3 (negativa), indica que hemos de vender tres bonos B. Es frecuente ver número decimales, e incluso menores que 1, eso no es importante, ya que estamos suponiendo que podemos trabajar con fracciones. Además si el valor de todas las celdas grises los multiplicas por cualquier número el bono que obtengas sigue siendo válido, ya que su TIR no cambia, puesto que lo que cambian son sus flujos de caja, pero de forma proporcional. Dos bonos proporcionales siempre tienen la misma TIR.

Son simplemente una herramienta de trabajo, lo importante es llegar al bono sintético que creamos y calcular su TIR.

A veces Solver da como solución todo ceros

En la versión de Excel 2010 se existe una opción nueva denominada:

Convertir variables sin restricciones en no negativas

Si esa opción esta marcada es posible que Solver en este problema y en otros similares de celdas grises el resultado que nos de sea poner todo como cero, y ese resultado no nos resuelve nada.

Para evitar que ponga todo como ceros se ha de desmarcar esta opción.

Conocido un tipo forward

Sean los siguientes bonos:
a. Bono A: bono cupón cero a un año de precio 100 € que se amortiza por 110 €.
b. Bono B: es un bono a dos años, de nominal 1.000 € , cupón del 9% anual y TIR rB.
Calcular el precio del bono B sabiendo que r12 =7,5%.

---

Método 1

La celda C23 es:

=+RAIZ((1+C20)*(1+C21))-1

La celda C38 es:

=+RAIZ((1+F32)*(1+C37))-1

En ambos casos estamos calculando r02 despejando de la fórmula:

Método 2

La fórmula que nos permite calcular el precio del bono B es esta

El primer cupón se divide entre (1+r01), y el segundo flujo de caja se divide entre (1+r12) para descontar un año (de t=2 hasta t=1), y también se dividen entre (1+r01) para descontar otro año (desde t=1 hasta t=0).

Método 3

Calcular la TIR de un bono conocido un tipo a plazo

En el mercado cotizan los siguientes bonos:
Bono A: Vencimiento a 7 años por el nominal (1.000 €). Cupón del 7% anual. Se adquiere a la par.
Bono B: Vencimiento a 7 años por el nominal (1.000 €). Cupón del 5% anual.
Bono C: Bono cupón cero a 7 años. TIR del 6%
Calcular la TIR del bono B.

---

Método 1

No conocemos el precio del bono B, y lo vamos a necesitar para calcular su TIR. Inicialmente nos lo inventamos, por ejemplo 900 €.

Construimos el Bono C combinando los bonos A y B para conseguir que sus flujos de caja intermedios se anulen. Para ello la celda E16 será:

=+$C$16*D16-$D$16*C16

y luego se copia hacia abajo, y hacia arriba.

Calculamos la TIR del bono C, y pedimos a Solver que consiga que sea del 6%, y que para conseguirlo nos calcule la celda verde (precio de B).

¿De donde sale la fórmula de la celda E27?

En la celda E27 utilizamos la expresión:

=+E22/(1+E26)^B22+E15

La fórmula viene de la Ley de Capitalización Compuesta, aplicada al bono C.

Cn=Co*(1+i)^n

En nuestro caso:

20000=13301*(1+0,06)^7

Esto se convierte en:

20000/(1+0,06)^7=13301

Y pasando lo 13.301 euros restando:

20000/(1+0,06)^7-13301=0

Esa expresión debería ser CERO, y es lo que le pedimos a Solver. Si Solver consigue que sea cero, nos aseguramos que el Bono C tiene una TIR del 6%, que es lo que indica el enunciado.

En realidad lo más cómodo es calcular la TIR del Bono C, y pedir a Solver que sea del 6%. Esto es lo que se hace en el método 2. Por tanto, si ves que esta fórmula no te resulta muy intuitiva, usa la TIR que es mucho más clara.

Método 2

Es método 2 es igual al método 1, salvo por la celda E33 donde queremos poner de manifiesto la forma de cálculo:

=70*D33-50*C33

Con esta expresión se ve muy bien, que lo que estamos haciendo es multiplicar dos cifras y luego restar ese mismo producto, por lo que el resultado es cero.

También prescindimos de pedir a Solver que haga la diferencia  cero, y en este caso le pedimos que directamente consiga que la rentabilidad sean del 6%.

Cálculo del precio de un bono usando la ETTI

En el mercado cotizan los siguientes bonos:
Bono A: Bono cupón cero a 1 año. TIR del 7%.
Bono B: Bono cupón explicito del 5% anual. Madura a los dos años y su TIR es del 6%.
Bono E: Bono cupón explícito del 7% anual. Madura a los dos años.
Calcular la TIR del bono E.

---

Método 1

Método 2

Método 3

Método 4

Con los bonos A y B construimos el bono C, que es un bono cupón cero a dos años.

Con la TIR de los bonos A y C construimos la ETTI, y calculamos el factor de descuento. La celda H47 es:

=+(1+G47)^-B47

Ahora calculamos el precio del bono E usando la ETTI. La celda F46 es:

=-SUMAPRODUCTO(H47:H48;F47:F48)