Sabemos que precio (P) y rentabilidad (r) se mueven en sentido contrario, pero nos gustaría saber en que magnitud. Nos gustaría poder comparar dos bonos y saber cuál de ellos es más sensible.
La curva siguiente nos muestra el comportamiento de estas dos magnitudes: Precio y Rentabilidad.
Esta curva no es una línea recta, por lo que no existe proporcionalidad o linealidad entre ambas magnitudes. Pero podemos tomar una aproximación lineal a la curva. Para ello tenemos que utilizar algo la matemáticas. Tenemos que derivar en una variable.
El precio de un bono es:
donde
- Ct son los Flujos de Caja que paga el Bono desde t=1 hasta t=n.
- r es la rentabilidad del Bono medida por su TIR
Ahora derivamos el Precio (P) respecto a la TIR (r).
D es la Duración de Macaulay
D/(1+r) es la denominada Duración Modificada
dr es la variación de la rentabilidad
Y el signo menos es importante, ya que nos indica que precio y rentabilidad se mueven en sentido contrario.
A efectos de aplicación práctica, los diferenciales anteriores se toman como incrementos, y así obtenemos una expresión, que ya no es una igualdad sino una expresión en términos aproximados.
La variación porcentual del precio en un bono es aproximadamente igual a la duración modificada multiplicado por la inversa de la variación de su rentabilidad.
La aproximación es tanto mejor cuanto menor sea la variación de la TIR que tomemos.
Gráficamente lo que estamos haciendo es la típica aproximación lineal a una curva en un punto, que es lo que vimos en su día cuando nos explicaron el concepto de derivada.
1 pb = 1% / 100
Un punto porcentual son 100 puntos básicos (100 pb).
Pongamos un ejemplo. Supongamos que un bono, cuya duración modificada es 3, experimenta una reducción en su rentabilidad de un 1%, esto es, 100 pb. En este caso la variación porcentual del precio es:
∆P/P ≈ - 3 * (-1%) = 3%
Esto quiere decir que la variación porcentual del precio (∆P/P) es del 3%. Por tanto, en términos aproximados el precio del bono se incrementa un 3% por cada 1% que caiga su rentabilidad.
Vemos perfectamente, gracias al signo menos, que precio y rentabilidad se mueven en sentido contrario.
Además, estamos comprobando que la duración modificada (D/(1+r)) hace el papel de multiplicador y que simplemente conociendo su valor podemos comparar dos bonos. De esta forma, si tenemos un bono, como el anterior, que llamaremos Bono A, cuya duración modificada de 3, y otro, Bono B, que la tiene de 10, es claro que el de mayor duración modificada será el más sensible. El Bono B ante una reducción del 1% en su TIR, experimentará un incremento porcentual del Precio del 10%, aproximadamente.
Estos sencillos cálculos mentales, permiten a los operadores de Renta Fija, conocer la sensibilidad de un bono simplemente mirando las pantallas de Reuters o de Bloomberg que les proporcionan este dato.


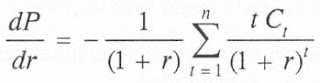




No hay comentarios:
Publicar un comentario